Như ở bài trước đã đề cập, phương pháp Fridrich hiện tại là phương pháp phổ biến nhất mà các người chơi Rubik trên thế giới đang sử dụng nhằm nâng cao tốc độc xoay Rubik.
Về Phương pháp Fridrich nói chung
Phương pháp Fridrich bao gồm 4 bước là
Bước 1: White Cross – Làm dấu cộng nâng cao
Bước 2: First two layers ( F2L) – Giải đồng thời tầng 1 và 2
Bước 3: Orienting the last layer ( OLL) – Định hướng lớp cuối cùng
Bước 4: Permutate the last layer ( PLL) – Hoán vị lớp cuối cùng
Như vậy sau khi qua 3 bước Giải dấu cộng nâng cao, Giải tầng 1 và 2 và Định hướng lớp cuối cùng, chúng ta sẽ được 1 khối Rubik hoàn thành được 2 lớp đầu tiên và mặt cuối cùng. Nếu như may mắn, các mặt cạnh của mặt cuối cùng sẽ về đúng vị trí của chúng, vậy thì Xong, bạn đã hoàn thành xong khối Rubik.
Tuy nhiên, phần lớn thì sau bước số 3, các mặt cạnh cần phải điều chỉnh lại để đúng màu với các ô giữa các bên. Do đó cần đến bước 4- Hoàn vị lớp cuối cùng.
Permutate the last layer ( PLL) – Hoán vị lớp cuối cùng
Bước thứ 4 và cũng là bước cuối cùng của phương pháp Fridrich nâng cao đó là hoán vị của lớp cuối cùng ( PLL). Mục tiêu của bước này là hoán vị lại các mảnh lớp cuối cùng để đảm bảo các mảnh cạnh trùng màu với các viên trung tâm cạnh và hoàn thành giải khối Rubik
Ở bước này chúng ta cần lưu ý 1 số kí:
X, Y ( x,y) là các phép quay cả khối Rubik
u: là hai lớp cuối cùng
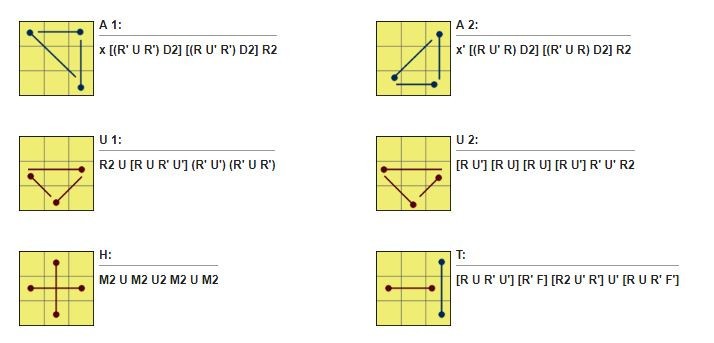
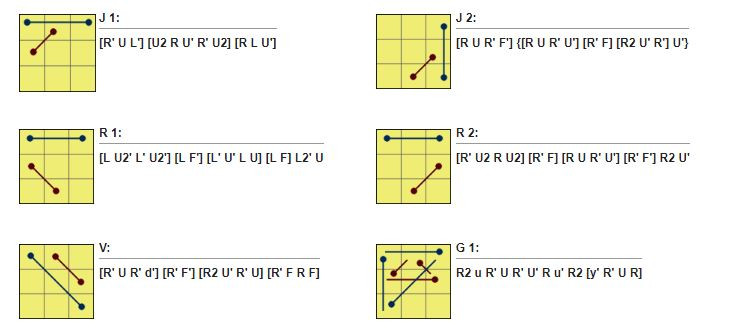
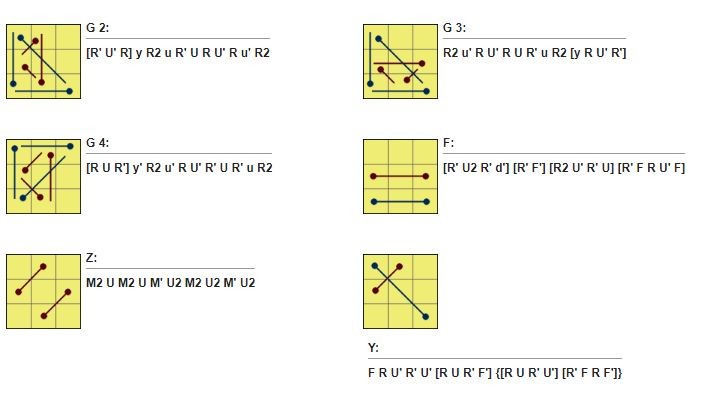
Trước tiên, hãy tự xoay lớp trên cùng để tự căn chỉnh được càng nhiều mảnh càng tốt, sau đó bạn tiến hành thực hiện theo 1 trong số 21 thuật toán dưới đây.
Nếu cảm thấy việc nhớ các thuật toán như vậy là quá nhiều, bạn nên thử phương pháp PLL 2look. Phương pháp này chỉ cần nhớ 6 thuật toán, nhưng dĩ nhiên là mất thêm nhiều thời gian hơn.
Ở đây, để dễ dàng định dạng các thuật toán, mình sẽ đặt tên cho các thuật toán, chúng khác nhau ở hình dạng các dấu chấm. Dấu chấm đại diện cho các mảnh lớp cuối cùng. Các dấu chấm được hoán vị cho nhau sẽ được liên kết bằng các dấu nối –
Ví dụ: tham khảo thuật toán A1, có hình khối Rubik thực tế như sau:

Các mảnh cần hoán vị lại là 3 mảnh góc được kí hiệu bằng 3 dấu chấm. Và 3 mảnh này sẽ hoán vị đổi chỗ cho nhau, nên ta liên kết chúng bởi các dấu gạch và tạo được hình như mô tả ở dưới.
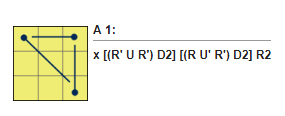
Cách xoay theo thuật toán A1 lần lượt qua các bước như sau:

Dưới đây là tổng hợp 21 công thức mà bạn cầm lắm rõ để giải bước cuối cùng của phương pháp Fridrich